The Evolution of Policy Optimization for Enhancing LLM Reasoning: From PPO to GRPO Variants

Preliminary

Basic Concepts

• 状态（State）：在时间步 $t$，状态 $s_{t}$ 是 prompt (a.k.a., query, question) $q$ 与 generated tokens $o_{<t}$ 的拼接。即，$s_{t} = [q,o_{<t}]$。其中：
  • $s_{1} = q \sim p_{\mathcal{Q}}$: 初态 $s_{1}$ 是从数据集 $p_{\mathcal{Q}}$ 中采样的 question $q$
  • $o_{<t}=[o_{1},o_{2},\ldots,o_{t-1}]$: 截止到当前时间步 $t$ 的 output
  • $s_{t+1} = [s_{t};o_{t}] = [q;o_{<t+1}]$: 下一状态 $s_{t+1}$
• 动作（Action）：在当前状态 $s_{t}$ 下，动作 $a_{t}$ 是从词汇表 $\mathcal{V}$ 中采样的 next token $o_{t}$。即，$a_{t} = o_{t}$
• 策略（Policy）：策略 $\pi$ 是 LLM 自身，其参数为 $\theta$。给定当前状态 $s_{t} = [q,o_{<t}]$，策略 $\pi(\cdot \mid q,o_{<t})$ 输出词汇表 $\mathcal{V}$ 中各 token 的概率分布。在 RHLF-PPO 的上下文中，还会出现以下策略：
  • $\pi_{\theta}$: 在 RL-tuning 阶段被持续优化的策略。其参数 $\theta$ 在每个 PPO epoch 中都会更新，代表了 LLM 在任意时刻的最新版本
  • $\pi_{\theta_{old}}$: 在本次迭代（第一个 PPO epoch）开始前，被设置为当前策略 $\pi_{\theta}$ 的一个副本；在本次迭代的所有 PPO epoch 中，其参数保持不变，用于计算 policy ratio $r_{t}(\theta)$；在本次迭代结束后，被丢弃；在下一次迭代开始前，再一次被设置为更新后的 $\pi_{\theta}$ 的副本
  • $\pi_{ref}$: 通常为 RL-tuning 前的 SFT 模型。在整个 RL-tuning 阶段，参数保持冻结，不进行更新。主要用于 KL 散度惩罚项的计算
• 状态转移（State Transition）：在当前状态 $s_{t}$ 下，采取动作 $o_{t}$ 后，系统唯一确定地转移到下一状态 $s_{t+1} = [s_{t};o_{t}] = [q;o_{<t+1}]$。即，$P(s_{t+1} \mid s_{t},o_{t}) = 1$
• 轨迹（Trajectory, a.k.a. Episode or Rollout）：一个完整的生成序列 $\tau$，是从 prompt $q$ 开始，经过一系列状态 - 动作对，直至生成结束符（EOS token）的完整序列。通常忽视 prompt $q$，表示为完整输出 $o = [o_{1},o_{2},\ldots,o_{|o|}]$

Reward and Return

传统 RL 中，奖励函数 $R(s_{t},a_{t},s_{t+1})$ 是环境固有的一部分，是客观且确定的。在 RLHF 中，奖励函数 $R(q,o_{\le t})$ 通常依赖于奖励模型（Reward Model, RM）。根据奖励信号的稀疏性，主要分为两种形式：结果奖励与过程奖励。

Outcome-based Reward

在这种设定下，奖励信号是稀疏的，仅在 response $o$ 生成结束后，结果奖励模型（Outcome Reward Model, ORM）才会计算出一个标量奖励分数 $r(q,o)$。因此，

• 对于轨迹中任意中间时刻 $t<|o|$，即时奖励 $R_{t} = 0$
• 只有在最后一个时间步 $t=|o|$，即时奖励 $R_{t} = r(q,o)$

形式化地，对于任意时间步 $t$，即时奖励可表示为：

$$R(q,o_{\le t}) = \mathbf{I}(o_{t} = [\text{EOS}])r(q,o)$$

其中，$\mathbf{I}(o_{t} = [\text{EOS}])$ 为指示函数，仅当 token $o_{t}$ 为结束符 EOS 时才会 $1$，否则均为 $0$

更进一步，对于任意时间步 $t$ 的回报 $G_{t}$ (假设折扣因子 $\gamma=1$) 均等于最终的整体奖励：

$$\begin{aligned} G_{t} &= \sum_{t^{\prime}=t}^{|o|} R_{t^{\prime}} \\ &= R(q,o_{\le t^{\prime}}) + R(q,o_{\le t^{\prime} +1}) + \cdots + R(q,o_{\le |o|}) \\ &= 0 + 0 + \cdots + R(q,o_{\le |o|}) \\ &= R(q,o_{\le |o|}) \\ &= r(q,o) \end{aligned}$$

虽然稀疏奖励实现简单，但存在信用分配问题（Credit Assignment Problem），难以判断哪个具体的 token 导致了最终奖励的高低。

Note

本文使用 $G_{t}$ 来表示回报。实际上，这与后文 GRPO, RLOO 中的 group 大小 $G$ 易混淆。还有一些工作使用 $R$ 表示回报，但为了与传统 RL 中的符号保持一致，我们仍然使用 $G_{t}$。

Process-based Reward

为了缓解稀疏奖励的信用分配问题，提供更稠密的信号，可以通过过程奖励模型（Process Reward Model, PRM）为生成过程中每个步骤 $t$ 都赋予奖励 $r(q,o_{\le t})$。因此，即时奖励 $R_{t} = R(q,o_{\le t}) = r(q,o_{\le t})$。显然，此时 $R(q,o_{\le t})$ 为 token-level reward。

在此设定下，一条完整轨迹 $o$ 的总回报为每一步奖励的累计和：

$$G(q,o) = \sum_{t=1}^{|o|} R(q,o_{\le t})$$

而从时间步 $t$ 开始的 reward-to-go 回报则为：

$$G_{t} = G(q,o_{\le t}) = \sum_{t^{\prime}=t}^{|o|}R(q,o_{\le t^{\prime}})$$

实际上，不论是稀疏奖励还是稠密奖励，回报都可以表示如上。

KL-Shaped Reward

在 RL-tuning 过程中，仅依赖于 RM 的信号引导，策略 $\pi_{\theta}$ 可能会发现并利用 RM 的漏洞，生成迎合 RM 偏好，但实际存在问题的文本，这一现象称为 Reward Hacking。进一步地，模型产生分布漂移（Distributional Shift）。为了解决这个问题，可以引入 KL 散度 $\mathbb{D}_{\text{KL}}(\pi_{\theta} \| \pi_{ref})$ 作为惩罚项，约束 $\pi_{\theta}$ 的输出概率分布不能偏离 $\pi_{ref}$ 太远。这种结合了外部奖励与 KL 散度的奖励形式，称为 KL-Shaped Reward。

当奖励模型为 ORM 时，复合奖励表示如下：

$$R(q,o_{\le t}) = \mathbf{I}(o_{t} = [\text{EOS}])r(q,o) - \beta \text{KL}_{t}$$

其中，$\beta$ 是控制 KL 惩罚力度的系数，$\text{KL}_{t}$ 是 KL 散度的近似。当使用 $k_{1}$ estimator 时，计算如下：

$$\text{KL}_{t} = \log \frac{\pi_{\theta_{old}}(o_{t} \mid q,o_{<t})}{\pi_{ref}(o_{t} \mid q,o_{<t})}$$

此时，由于奖励函数中加入了 KL 散度，稀疏奖励变得稠密化，PPO 使用的就是这种 token-level 奖励。而 RLOO 为了使奖励信号再次稀疏化，将整个序列的 KL 惩罚聚合起来，只在最后一个时间步与 ORM 奖励一同发放：

$$R(q,o) = r(q,o) - \beta \sum_{t=1}^{|o|} \text{KL}_{t}$$

特别地，在 RL-tuning reasoning model 中，ORM 通常为 rule-based verifier，通常不会引起分布漂移。此时，将移除 KL 惩罚项，省去了 Ref Model 的加载。

Objective Function

在 RLHF 中，我们的目标是最大化 $J(\theta)$:

$$\max_{\theta}J(\theta) = \mathbb{E}_{q \sim p_{\mathcal{Q}}} \Big[\mathbb{E}_{o \sim \pi_{\theta}(\cdot \mid q)} \big[G(q, o)\big]\Big]$$

其中：

• $G(q,o) = \sum_{t=1}^{|o|}R(q,o_{\le t})$ 是整条轨迹上的回报
• $R(q,o_{\le t})$ 是 response $o$ 中第 $t$ 个 token 的 token-level reward

接下来，策略梯度推导如下：

$$\begin{aligned} \nabla_{\theta} J(\theta) &= \mathbb{E}_{q \sim p_{\mathcal{Q}}}\bigg[ \mathbb{E}_{o \sim \pi_{\theta}(\cdot \mid q)}\big[ \nabla_{\theta} \log \pi_{\theta}(o \mid q) G(q, o)\big]\bigg] \\ &= \mathbb{E}_{q \sim p_{\mathcal{Q}}}\bigg[ \mathbb{E}_{o \sim \pi_{\theta}(\cdot \mid q)}\Big[ \nabla_{\theta} \sum_{t=1}^{|o|} \log \pi_{\theta}(o_{t} \mid q, o_{<t}) G(q, o)\Big]\bigg] \\ &= \mathbb{E}_{q \sim p_{\mathcal{Q}}}\bigg[ \mathbb{E}_{o \sim \pi_{\theta}(\cdot \mid q)}\Big[ \sum_{t=1}^{|o|} \nabla_{\theta} \log \pi_{\theta}(o_{t} \mid q, o_{<t}) \sum_{t^{\prime}=t}^{|o|} R(q, o_{\le t^{\prime}})\Big]\bigg] \\ &= \mathbb{E}_{q \sim p_{\mathcal{Q}}}\Bigg[ \mathbb{E}_{o \sim \pi_{\theta}(\cdot \mid q)}\bigg[ \sum_{t=1}^{|o|} \nabla_{\theta} \log \pi_{\theta}(o_{t} \mid q, o_{<t}) \bigg( \sum_{t^{\prime}=t}^{|o|} R(q, o_{\le t^{\prime}}) - b(q, o_{<t}) \bigg) \bigg]\Bigg] \end{aligned}$$

其中，$b(q,o_{<t})$ 称为 baseline，通常用于减少策略梯度估计的方差。可以证明，当 baseline 不依赖于动作 $o_{t}$ 时，其期望为 $0$，不会影响策略梯度的近似：

$$\mathbb{E}_{o_{t} \sim \pi_{\theta}(\cdot \mid q,o_{<t})} \Big[ \nabla_{\theta} \log \pi_{\theta}(o_{t} \mid q,o_{<t}) b(q,o_{<t}) \Big] = 0$$

通常，baseline 可以设置为未来期望回报，在传统 RL 中表示为状态价值 $V^{\pi}(s_{t})$:

$$b(q,o_{<t}) = V^{\pi}(q,o_{<t}) = \mathbb{E}_{o_{\ge t} \sim \pi_{\theta}(\cdot \mid q,o_{<t})} \bigg[ \sum_{t^{\prime}=t}^{|o|} R(q, o_{\le t^{\prime}}) \bigg]$$

为了简化表示，我们定义 $t$ 时刻的优势 $A_{t}$:

$$A_{t} = G_{t} - b(q,o_{<t}) = \sum_{t^{\prime}=t}^{|o|} R(q, o_{\le t^{\prime}}) - b(q, o_{<t})$$

此时，策略梯度可以简化为：

$$\nabla_{\theta} J(\theta) = \mathbb{E}_{q \sim p_{\mathcal{Q}},o \sim \pi_{\theta}(\cdot \mid q)}\Bigg[ \sum_{t=1}^{|o|} \nabla_{\theta} \log \pi_{\theta}(o_{t} \mid q, o_{<t}) A_{t} \Bigg]$$

不同的算法使用不同的 advantage estimator $\hat{A}_{t}$，对策略梯度的近似也会存在不同的 bias-variance trade-off

REINFORCE

REINFORCE 使用轨迹中实际采样得到的真实奖励和来近似回报（a.k.a., 蒙特卡洛回报）。具体实现中，可以不使用 value network 来近似 baseline。REINFORCE 的特点是无偏高方差：

• 无偏：蒙特卡洛回报是对策略梯度的无偏估计
• 高方差：蒙特卡洛回报是一个很长的随机变量 $R$ 的累计和，从而导致梯度估计的高方差

PPO: Proximal Policy Optimization

PPO 的奖励信号通常采用典型的 token-level 的 KL-shaped reward:

$$R(q,o_{\le t}) = \mathbf{I}(o_{t} = [\text{EOS}])r(q,o) - \beta \text{KL}_{t}$$

其中，$r(q,o)$ 是 ORM 对整个轨迹的打分。

PPO 采用重要性网络，希望复用旧策略 $\pi_{\theta_{old}}$ 采集的数据来多次更新当前策略 $\pi_{\theta}$。其目标是最大化 $J(\theta)$:

$$\begin{aligned} J(\theta) = \mathbb{E}_{q \sim p_{\mathcal{Q}}}\Bigg[ \mathbb{E}_{o \sim \pi_{\theta_{old}}(\cdot \mid q)} \bigg[ \sum_{t=1}^{|o|} \min\Big( r_{t}(\theta) \hat{A}_{t}, \mathrm{clip}\big(r_{t}(\theta),1-\epsilon,1+\epsilon\big)\hat{A}_{t} \Big)\bigg] \Bigg] \end{aligned}$$

其中，$\mathrm{clip}\big(r_{t}(\theta),1-\epsilon,1+\epsilon\big)$ 是一个裁剪函数，用于将 policy ratio $r_{t}(\theta)$ 限制在 $[1-\epsilon,1+\epsilon]$ 的区间内。这里的 $\epsilon$ 是一个超参数，定义信任区域的大小。$r_{t}(\theta)$ 表示如下：

$$r_{t}(\theta) = \frac{\pi_{\theta}(o_{t} \mid q,o_{<t})}{\pi_{\theta_{old}}(o_{t} \mid q,o_{<t})}$$

优势使用 GAE $\hat{A}_{t}^{\mathrm{GAE}(\gamma,\lambda)}$ 近似，其中 $\lambda$ 用于平衡 bias-variance。同时，GAE 的计算需要使用 value network 来近似状态价值，因此 PPO 本质上是一个 A2C 框架。后续的大量工作为了节省显存占用，设计不同的 baseline 来丢弃 value network。

RLOO: REINFORCE Leave One Out

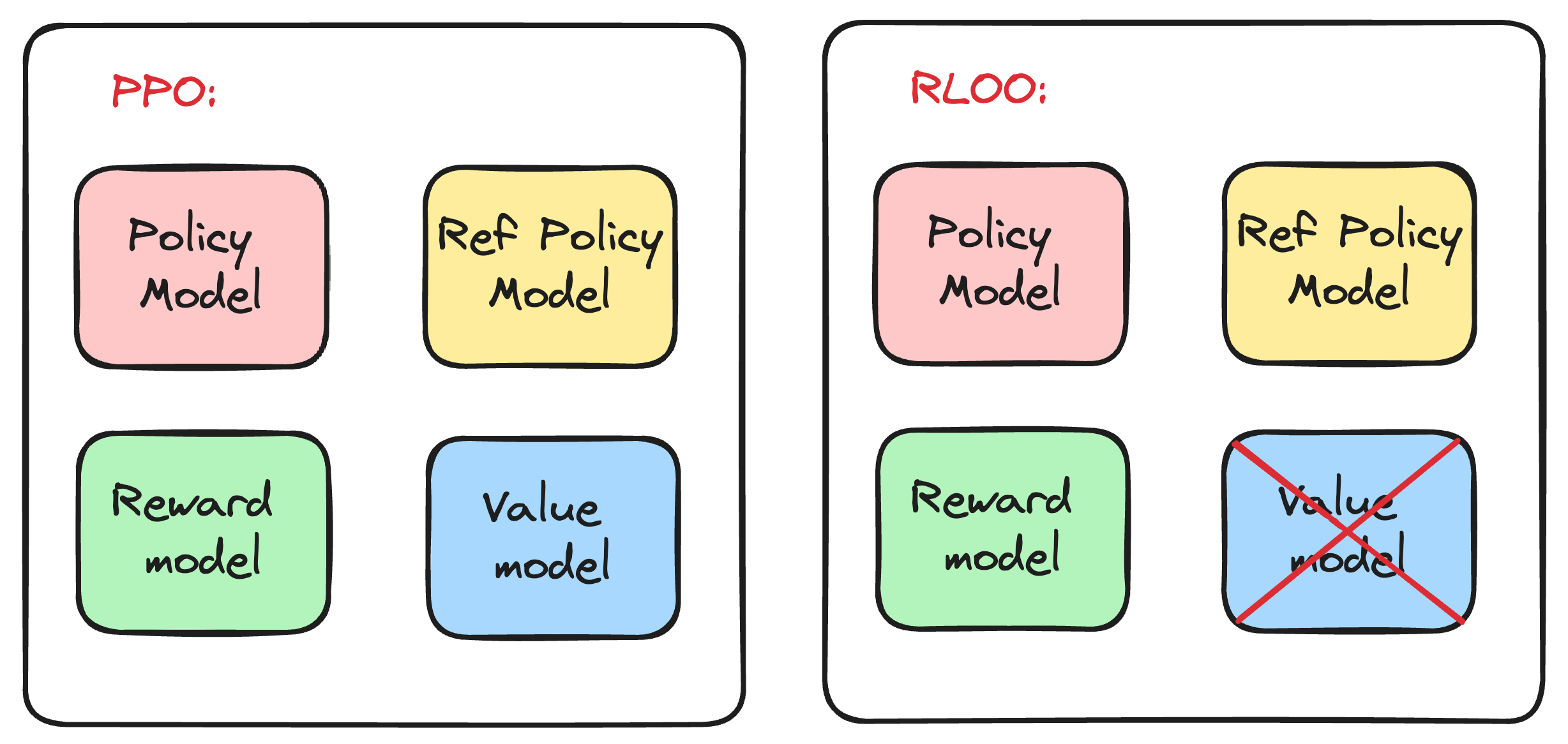
RLOO 的核心动机在于丢弃 PPO 中的 value network，从而节省显存占用，如下图所示。

baseline 一般被设计为状态价值，这通常需要 value network 来近似。RLOO 通过对单个 prompt $q$ 采样多个（$G$ 个）在线样本 $\{o_{i}\}_{i=1}^{G}$ 来计算 baseline，以减小方差。在正式介绍 RLOO baseline 前，先对比其与 PPO 的奖励信号。

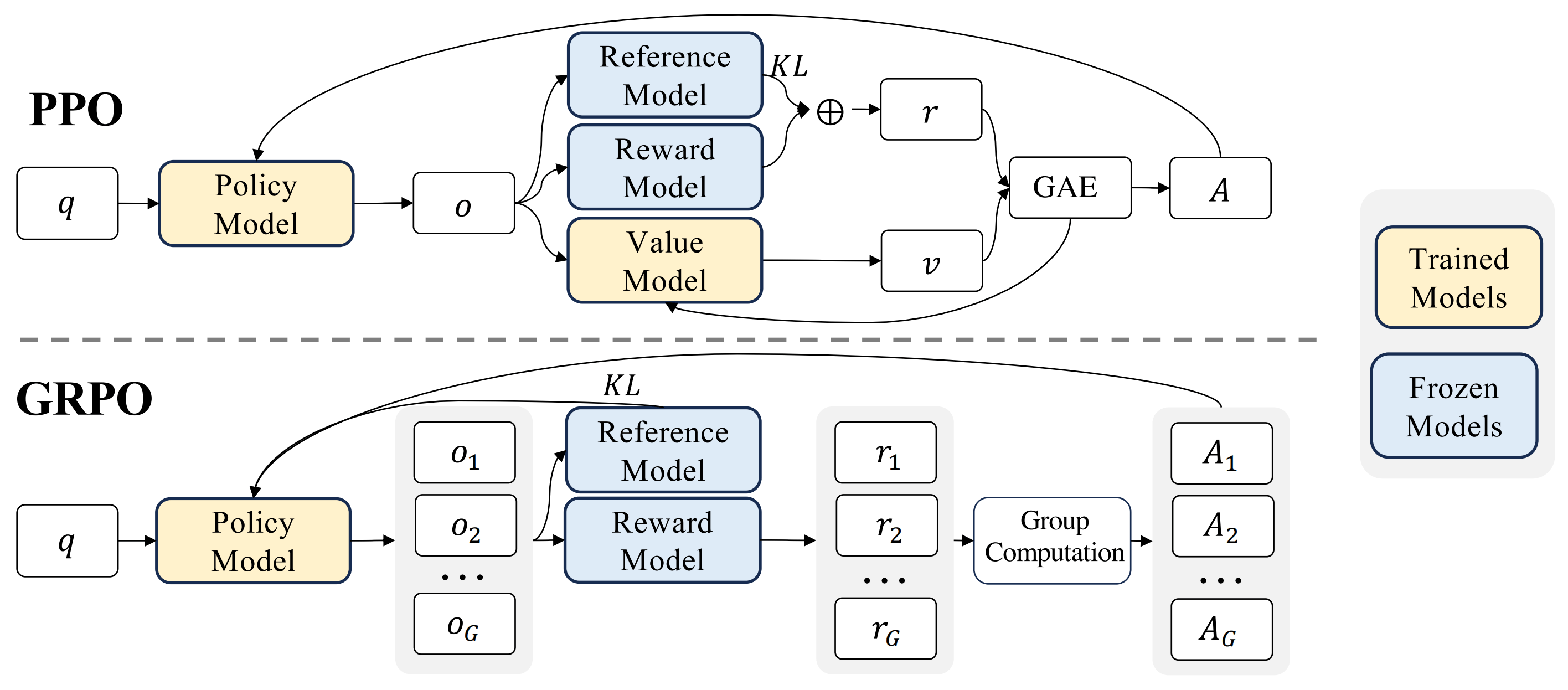
RLOO 与 PPO 不同，后者采用 token-level 的 KL-shaped reward 奖励信号，而前者采用 response-level 的稀疏奖励信号。换句话说，对于一条 response，只有唯一的即时奖励 $R(q,o)$ 与回报 $G(q,o)$。具体来说，RLOO 通过将整个序列的 KL 惩罚聚合，同 ORM 打分加和构成 response-level reward:

$$R(q,o) = r(q,o) - \beta \sum_{t=1}^{|o|} \text{KL}_{t}$$

下图对比了 PPO 和 RLOO 的奖励计算：

RLOO 将 group 中的样本 $o_{i}$ 的 baseline $b(q,o_{i})$ 设置为剩余 $G-1$ 个样本回报（实际上也是奖励）的均值：

$$\begin{aligned} b(q,o_{i}) &= \frac{1}{G-1} \sum_{j=1,j \ne i}^{G} G(q,o_{j}) \\ &= \frac{1}{G-1} \sum_{j=1,j \ne i}^{G} R(q,o_{j}) \end{aligned}$$

由于剔除了自身样本的奖励，因此 $b(q,o_{i})$ 不依赖于动作 $o_{i,t}$，因此其期望值为 $0$，RLOO 对策略梯度的估计仍是无偏的。这里 $o_{i,t}$ 指的是 group 中的 response $o_{i}$ 在任意时间步 $t$ 采样的 token。接下来，给出 RLOO 的 advantage estimator:

$$\begin{aligned} \hat{A}_{i} &= G(q,o_{i}) - b(q,o_{i}) \\ &= R(q,o_{i}) - \frac{1}{G-1} \sum_{j=1,j \ne i}^{G} R(q,o_{j}) \\ &= R(q,o_{i}) - \frac{1}{G-1} \bigg( \sum_{j=1}^{G} R(q,o_{j}) - R(q,o_{i}) \bigg)\\ &= \frac{G}{G-1} R(q,o_{i}) - \frac{1}{G-1} \sum_{j=1}^{G} R(q,o_{j}) \\ &= \frac{G}{G-1} \bigg( R(q,o_{i}) - \frac{1}{G} \sum_{j=1}^{G} R(q,o_{j}) \bigg) \end{aligned}$$

直观地，优势 $\hat{A}_{i}$ 表示当前输出 $o_{i}$ 的奖励比当前 group 中其他输出 $G-1$ 个输出 $o_{j}(j \ne i)$ 的平均奖励高多少：

• 如果 $\hat{A}_{i} > 0$，说明 $o_{i}$ 是一个较好的输出，我们要增大其每一个 token 的概率
• 如果 $\hat{A}_{i} < 0$，说明 $o_{i}$ 是一个较坏的输出，我们要减小其每一个 token 的概率

这里也可以看出与 PPO 的 GAE 优势的差距：PPO GAE 是 token-level 的优势，而 RLOO 将 $o_{i}$ 中每个 token $o_{i,t}$ 的贡献一视同仁。即，$\hat{A}_{i,t} = \hat{A}_{i}$。

最后，RLOO 策略梯度计算如下：

$$\begin{aligned} \nabla_{\theta} J(\theta) &= \mathbb{E}_{q \sim p_{\mathcal{Q}}}\Bigg[ \mathbb{E}_{\{o_{i}\}_{i=1}^{G} \sim \pi_{\theta}(\cdot \mid q)}\bigg[ \frac{1}{G} \sum_{i=1}^{G} \sum_{t=1}^{|o_{i}|} \nabla_{\theta} \log \pi_{\theta}(o_{i,t} \mid q, o_{i,<t}) \hat{A}_{i} \bigg]\Bigg]\\ &= \mathbb{E}_{q \sim p_{\mathcal{Q}}}\Bigg[ \mathbb{E}_{\{o_{i}\}_{i=1}^{G} \sim \pi_{\theta}(\cdot \mid q)}\bigg[ \frac{1}{G} \sum_{i=1}^{G} \hat{A}_{i} \nabla_{\theta} \log \pi_{\theta}(o_{i} \mid q) \bigg]\Bigg]\\ &= \mathbb{E}_{q \sim p_{\mathcal{Q}}}\Bigg[ \mathbb{E}_{\{o_{i}\}_{i=1}^{G} \sim \pi_{\theta}(\cdot \mid q)}\bigg[ \frac{1}{G} \sum_{i=1}^{G} \frac{G}{G-1} \bigg( R(q,o_{i}) - \frac{1}{G} \sum_{j=1}^{G} R(q,o_{j}) \bigg) \nabla_{\theta} \log \pi_{\theta}(o_{i} \mid q) \bigg]\Bigg]\\ &= \mathbb{E}_{q \sim p_{\mathcal{Q}}}\Bigg[ \mathbb{E}_{\{o_{i}\}_{i=1}^{G} \sim \pi_{\theta}(\cdot \mid q)}\bigg[ \frac{1}{G-1} \sum_{i=1}^{G} \bigg( R(q,o_{i}) - \frac{1}{G} \sum_{j=1}^{G} R(q,o_{j}) \bigg) \nabla_{\theta} \log \pi_{\theta}(o_{i} \mid q) \bigg]\Bigg] \end{aligned}$$

从第一个等式也可看出，RLOO 策略梯度估计的最小计算单元不是单个样本，而是整个 group。

Note

GRPO 与 RLOO 都是同期思路类似的工作，为了保持全文符号的一致性，我们这里是用 group $G$ 来表述。实际上，这一表述源自 GRPO

ReMax

ReMax 是 RLOO 的同期工作，动机也是为了丢弃 PPO 中的 value network，其奖励信号也是 response-level (a.k.a., trajectory-level)。与 RLOO 的差异主要体现在 baseline 的设计。

对于每个 prompt $q \sim p_{\mathcal{Q}}$, RLOO 从 $\pi_{\theta}(\cdot \mid q)$ 采样独立同分布的 $G$ 个 output $\{o_{i}\}_{i=1}^{G}$，而 ReMax 仅生成两个序列：

• 随机序列：$o \sim \pi_{\theta}(\cdot \mid q)$
• 贪婪序列：$o_{\text{max}}$，通过每次贪婪选择概率最高的 token 组成，即：$o_{\text{max},t} = \arg\max_{w} \pi_{\theta}(w \mid q,o_{\text{max},<t})$

ReMax baseline 定义为贪婪序列的回报（实际上也是奖励）$R(q,o_{\text{max}})$。由于 $o_{\text{max}}$ 与随机序列 $o$ 的各 token 无关，因此其对策略梯度的估计是无偏的。论文中详细证明了该 baseline 能有效降低策略梯度估计的方差，本文不再展开。

GRPO: Group Relative Policy Optimization

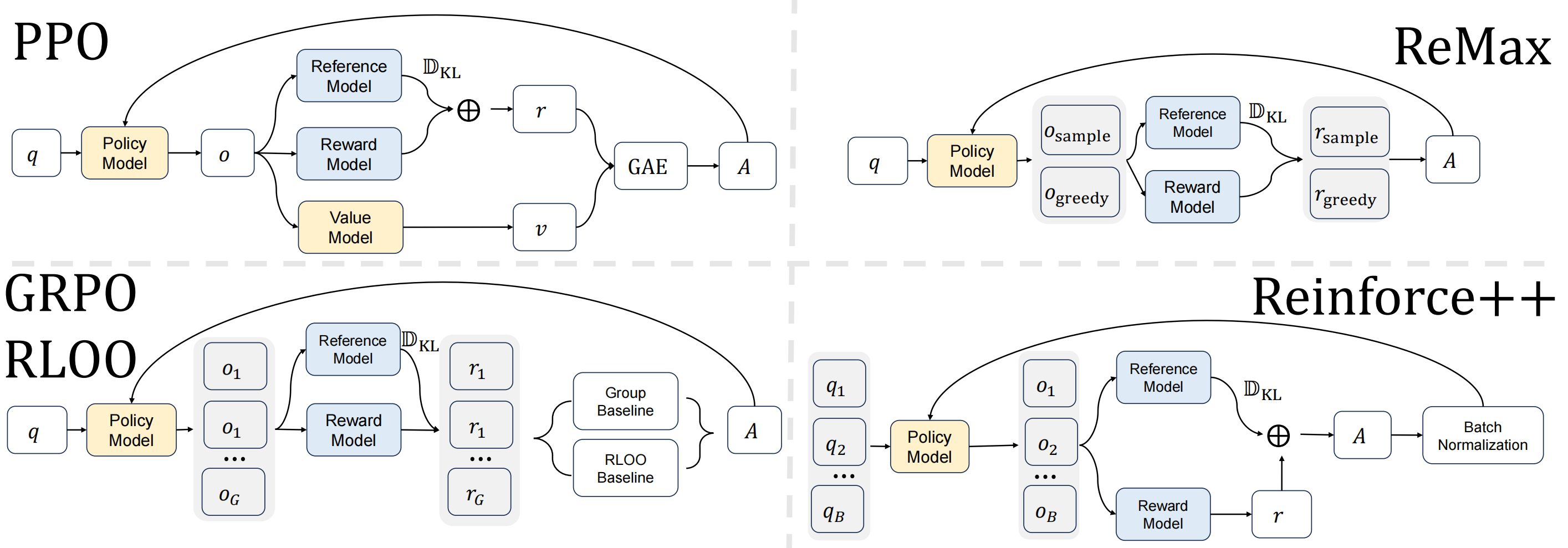
GRPO 也是 ReMax, RLOO 的同期工作，其基于 PPO 算法，如上图所示。其目标函数如下：

$$\begin{aligned} J(\theta) &= \mathbb{E}_{q \sim p_{\mathcal{Q}},\{o_{i}\}_{i=1}^{G} \sim \pi_{\theta_{old}}(\cdot \mid q)} \\ & \frac{1}{G}\sum_{i=1}^{G} \frac{1}{|o_{i}|}\sum_{t=1}^{|o_{i}|} \bigg\{ \min\Big( r_{i,t}(\theta) \hat{A}_{i,t}, \mathrm{clip}\big(r_{i,t}(\theta),1-\epsilon,1+\epsilon\big)\hat{A}_{i,t} \Big) - \beta \mathbb{D}_{\text{KL}}\big[\pi_{\theta}(\cdot \mid q) \| \pi_{ref}(\cdot \mid q)\big] \bigg\} \end{aligned}$$

其中，policy ratio $r_{i,t}(\theta)$ 表示如下：

$$r_{i,t}(\theta) = \frac{\pi_{\theta}(o_{i,t} \mid q,o_{i,<t})}{\pi_{\theta_{old}}(o_{i,t} \mid q,o_{i,<t})}$$

GRPO group 中 output $o_{i}$ 的第 $t$ 个 token $o_{i,t}$ 的优势近似为该 token 的回报 $G(q,o_{i,\le t})$，而回报是自 $t$ 时刻其的累计奖励和。GRPO 的核心思想是对奖励进行 normalization，这里对奖励信号分两种情形进行探讨：结果监督与过程监督。

当奖励信号是 response-level 的结果监督时，$G(q,o_{i,\le t}) = G(q,o_{i}) = \tilde{R}(q,o_{i})$，group normalized advantage 表示如下：

$$\hat{A}_{i} = G(q,o_{i}) = \tilde{R}(q,o_{i}) = \frac{R(q,o_{i}) - \mathrm{mean}(\{ R(q,o_{1}),\ldots,R(q,o_{G}) \})}{\mathrm{std}(\{R(q,o_{1}),\ldots,R(q,o_{G})\})}$$

其中，$\tilde{R}(q,o_{i})$ 是 group normalized reward。同时可以看到，优势（同时包括回报，即时奖励）中剔除了时间维度，因为对所有 token 一视同仁，即：$\hat{A}_{i,t}=\hat{A}_{i}$。此外，即时奖励直接由 ORM 直接给出，即，$R(q,o_{i})=r(q,o_{i})$。这里没有使用 KL-shaped reward，是因为 GRPO 将 KL 惩罚直接加入到了目标函数中，后面会详细讲解。

当奖励信号是 token-level 的过程监督时，reward 需要对所有 group 中各时间步进行归一化，则参与归一化计算的所有奖励信号可以表示为一个集合 $\mathbf{R} = \big\{\{R(q,o_{1,\le 1}),\ldots,R(q,o_{1,\le |o_{1}|})\},\ldots,\{R(q,o_{G,\le 1}),\ldots,R(q,o_{G,\le |o_{G}|})\}\big\}$，集合大小为 $\sum_{i=1}^{G}|o_{i}|$。接着，group normalized reward 表示如下：

$$\tilde{R}(q,o_{i,\le t}) = \frac{R(q,o_{i,\le t}) - \mathrm{mean}(\mathbf{R})}{\mathrm{std}(\mathbf{R})}$$

其中，即时奖励 $R(q,o_{i,\le t})$ 由 PRM 直接给出，即，$R(q,o_{i,\le t}) = r(q,o_{i,\le t})$。最后，优势仍然使用回报近似：

$$\hat{A}_{i,t} = G(q,o_{i,\le t}) = \sum_{t^{\prime} = t}^{|o_{i}|} \tilde{R}(q,o_{i,\le t^{\prime}})$$

除了优势近似外，还有几处与标准 PPO 的差异：

• Length Normalization: $1/|o_{i}|$ 对 output $o_{i}$ 的长度进行归一化。实际上，大部分 PPO 的实现也进行了归一化，但标准的 PPO 不包含该项。这一项也引入了一些 bias, Dr. GRPO 对此进行了讨论与改进
• KL Penalty: 直接将 KL 惩罚加入目标函数，而非采用 KL-shaped reward。因此，其目标函数的形式类似 PPO-Clip 与 PPO-Penalty 的统一

GRPO 目标函数中的 KL 散度使用 $k_{3}$ estimator:

$$\hat{\mathbb{D}}_{\text{KL}}\big[\pi_{\theta}(\cdot \mid q) \| \pi_{ref}(\cdot \mid q)\big] = \frac{\pi_{ref}(o_{i,t} \mid q,o_{i,<t})}{\pi_{\theta}(o_{i,t} \mid q,o_{i,<t})} - \log \frac{\pi_{ref}(o_{i,t} \mid q,o_{i,<t})}{\pi_{\theta}(o_{i,t} \mid q,o_{i,<t})} - 1$$

对于 GRPO bias 的讨论，见 Dr. GRPO 一节。

Dr. GRPO: Group Relative Policy Optimization Done Right

此前，我们发现 GRPO 与 RLOO 的优势计算十分相似，Dr. GRPO 基于 GRPO 进行优化，并揭示了优化后的优势计算与 RLOO 的联系。首先，我们对比 GRPO，给出 Dr. GRPO 的目标函数：

$$\begin{aligned} J(\theta) &= \mathbb{E}_{q \sim p_{\mathcal{Q}},\{o_{i}\}_{i=1}^{G} \sim \pi_{\theta_{old}}(\cdot \mid q)} \\ & \frac{1}{G}\sum_{i=1}^{G} {\color{red}\xcancel{\frac{1}{|o_{i}|}}} \sum_{t=1}^{|o_{i}|} \bigg\{ \min\Big( r_{i,t}(\theta) \hat{A}_{i,t}, \mathrm{clip}\big(r_{i,t}(\theta),1-\epsilon,1+\epsilon\big)\hat{A}_{i,t} \Big) {\color{red}\xcancel{- \beta \mathbb{D}_{\text{KL}}\big[\pi_{\theta}(\cdot \mid q) \| \pi_{ref}(\cdot \mid q)\big]}} \bigg\} \end{aligned}$$

其中

$$\hat{A}_{i} = \frac{R(q,o_{i}) - \mathrm{mean}(\{ R(q,o_{1}),\ldots,R(q,o_{G}) \})}{\color{red}\xcancel{\mathrm{std}(\{R(q,o_{1}),\ldots,R(q,o_{G})\})}}$$

为了简化分析，我们不妨假设只有结果奖励信号，即：$\hat{A}_{i,t} = \hat{A}_{i}$。实际上，过程奖励信号的场景分析也同理。

对比 GRPO 发现，Dr. GRPO 移除了目标函数中的 KL 惩罚，更核心的是，移除了 $\color{red}1/|o_{i}|$ 与 $\color{red}\mathrm{std}(\{R(q,o_{1}),\ldots,R(q,o_{G})\})$ 归一化项。这一点源于 GRPO 中的这两个归一化项引入了两个 biases:

• Response-level length bias: 源于 $\color{red}1/|o_{i}|$，分为两种情况讨论：
  • 当 $\hat{A}_{i} > 0$，即 response $o_{i}$ 正确时：更短的 response 将获得更大幅度的梯度更新，因为其归一化后权重更高。这可能鼓励模型生成更简短的正确回复
  • 当 $\hat{A}_{i} < 0$，即 response $o_{i}$ 错误时：更长的 response 受到的惩罚较小，因为其权重被长度稀释。这可能鼓励模型生成更长的错误回复
• Question-level difficulty bias: 源于 $\color{red}\mathrm{std}(\{R(q,o_{1}),\ldots,R(q,o_{G})\})$。奖励标准差较低的问题（e.g., 非常容易或非常困难的问题，因为奖励大多为 $1$ 或 $0$）会获得更高的优化权重

最后，证明 Dr. GRPO 优势的无偏性，从 RLOO 优势出发：

$$\begin{aligned} \hat{A}_{i}^{\text{RLOO}} &= \frac{G}{G-1} \bigg( R(q,o_{i}) - \frac{1}{G} \sum_{j=1}^{G} R(q,o_{j}) \bigg)\\ &= \frac{G}{G-1} \hat{A}_{i}^{\text{Dr.GRPO}} \end{aligned}$$

由于 RLOO 优势对策略梯度的近似是无偏的，我们只需证明 Dr. GRPO 与 RLOO 优势等价即可。我们发现，当 group size $G \to \infty$ 时，$\hat{A}_{i}^{\text{Dr.GRPO}} \to \hat{A}_{i}^{\text{RLOO}}$。实际上，$G/(G-1)$ 这一因子可以在 RL-tuning 被学习率吸收。因此，我们可以认为 Dr. GRPO 优势对策略梯度的近似也是无偏的。

REINFORCE++

如上图所示，REINFORCE++ 基于 GRPO 进行改进，核心思想在于对优势函数使用 batch normalization，目标函数仍然是 PPO loss。其奖励信号与 PPO 一致，采用 token-level KL-shaped reward，表示如下：

$$R(q,o_{\le t}) = \mathbf{I}(o_{t} = [\text{EOS}])r(q,o) - \beta \text{KL}_{t}$$

其中，$\text{KL}_{t}$ 是 KL 散度的近似，$r(q,o)$ 是 ORM 对 $[q,o]$ 的打分。如果采用 PRM，则 $R(q,o_{\le t}) = r(q,o_{\le t})$。标准 REINFORCE++ 使用 $k_{1}$ estimator 时，计算如下：

$$\text{KL}_{t} = \log \frac{\pi_{\theta_{old}}(o_{t} \mid q,o_{<t})}{\pi_{ref}(o_{t} \mid q,o_{<t})}$$

标准 REINFORCE++ 移除了 GRPO 中的 group，沿用 PPO 的算法步骤：

1. 从 prompt dataset $p_{\mathcal{Q}}$ 中采样一个 batch 的 prompt $\{q^{(n)}\}_{n=1}^{N} \sim p_{\mathcal{Q}}$
2. 对于每个 prompt $q^{(n)}$，从 old policy 中采样一个 output $o^{(n)} \sim \pi_{\theta_{old}}(\cdot \mid q^{(n)})$
3. 为 batch 中每个 output $o^{(n)}$ 计算各时间步 $t$ 的即时奖励 $R(q^{(n)},o_{\le t}^{(n)})$ 与优势 $\hat{A}_{t}^{(n)}$

其中，优势使用 global batch normalization 进行计算。类似 GRPO，我们先将参与归一化计算的所有奖励信号表示为一个集合 $\mathbf{R} = \big\{\{R(q^{(1)},o_{\le 1}^{(1)}),\ldots,R(q^{(1)},o_{\le |o^{(1)}|}^{(1)})\},\ldots,\{R(q^{(N)},o_{\le 1}^{(N)}),\ldots,R(q^{(N)},o_{\le |o^{(N)}|}^{(N)})\}\big\}$，集合大小为 $\sum_{n=1}^{N}|o^{(n)}|$。接着，给出优势归一化公式：

$$\hat{A}_{t}^{(n)} = \frac{R(q^{(n)},o_{\le t}^{(n)}) - \mathrm{mean}(\mathbf{R})}{\mathrm{std}(\mathbf{R})}$$

这里也看出与 GRPO 的显著区别，REINFORCE++ 沿用 PPO，为每个 prompt 仅采样一个 response，而 GRPO 是采样一组 response，这也造成了 normalization 方式的差异。

Note

这里计算优势时，使用的仍然是即时奖励，而非回报。当 GRPO 使用 token-level reward 时，优势使用回报近似，而非即时奖励。

实际上，为了支持 multi-response 的场景，REINFORCE+±baseline 这一变体被提出。首先，为 batch 所有样本计算各自的 group normalized advantage $\hat{A}_{i,t}^{(n)}$。这里为了保持符号的简洁性，我们省略上标 $(n)$，因为 group normalization 都是 prompt-specific 的。公式表示如下：

$$\hat{A}_{i,t} = R(q,o_{i,\le t}) - \mathrm{mean}\big(\big\{\{R(q,o_{1,\le 1}),\ldots,R(q,o_{1,\le |o_{1}|})\},\ldots,\{R(q,o_{G,\le 1}),\ldots,R(q,o_{G,\le |o_{G}|})\}\big\}\big)$$

类似 Dr. GRPO，这里的 group normalization 并不会除以标准差。最后，与标准 REINFORCE++ 一致，进一步计算 global batch normalized advantage。这里不再给出具体计算公式，因为符号表示较复杂。需要注意的是，参与均值与标准差运算的样本数量为 $\sum_{n=1}^{N} \sum_{i=1}^{G} |o_{i}^{(n)}|$

DAPO: Decouple Clip and Dynamic sAmpling Policy Optimization

DAPO 基于 GRPO 算法，针对 long-CoT RL 场景进行改进。对比 GRPO，其目标函数如下：

$$\begin{aligned} J(\theta) &= \mathbb{E}_{(q,a) \sim p_{\mathcal{Q}},\{o_{i}\}_{i=1}^{G} \sim \pi_{\theta_{old}}(\cdot \mid q)} \\ & {\color{red}\frac{1}{\sum_{i=1}^{G}|o_{i}|} \xcancel{\frac{1}{G}}}\sum_{i=1}^{G} {\color{red}\xcancel{\frac{1}{|o_{i}|}}} \sum_{t=1}^{|o_{i}|} \bigg\{ \min\Big( r_{i,t}(\theta) \hat{A}_{i,t}, \mathrm{clip}\big(r_{i,t}(\theta),1-\epsilon_{\text{low}},1+\epsilon_{\text{high}}\big)\hat{A}_{i,t} \Big) {\color{red}\xcancel{- \beta \mathbb{D}_{\text{KL}}\big[\pi_{\theta}(\cdot \mid q) \| \pi_{ref}(\cdot \mid q)\big]}} \bigg\} \\ & {\color{red}\text{s.t.}\quad 0 < \Big| \{ o_{i} \mid \mathrm{is\_equivalent}(a,o_{i}) \} \Big| < G} \end{aligned}$$

其中，$(q,a) \sim p_{\mathcal{Q}}$ 指从数据集 $p_{\mathcal{Q}}$ 中采样 question-answer pair。上式中红色部分是与 GRPO 的差异。首先，DAPO 移除了 KL 惩罚，这是由于 RL 场景差异导致：

• RLHF 中，我们的目标是在不偏离初始模型太远的情况下，微调模型使之与人类偏好对齐
• Long-CoT Reasoning RL 中，对于一个复杂的数学或逻辑问题，初始模型可能根本不知道如何解答。我们希望鼓励模型探索，生成 long-CoT，这个过程中，模型的概率分布会发生较大变化，因此不需要 KL 惩罚的限制

剩余的改进归纳为四点：

Techniques	Goals	Formulation
Clip-Higher	鼓励探索，避免熵坍缩	$\epsilon_{\text{low}}$,$\epsilon_{\text{high}}$
Dynamic Sampling	持续提供有效梯度，加快收敛	$\text{s.t.}\quad 0 < \vert \{ o_{i} \mid \mathrm{is\_equivalent}(a,o_{i}) \} \vert < G$
Token-Level Policy Gradient Loss	避免较长序列梯度的稀释	$1 / \sum_{i=1}^{G}\vert o_{i} \vert$
Overlong Reward Shaping	降低奖励噪音	$R_{\text{length}}$

在正式解读前，先明确其奖励信号。为了避免 reward hacking 问题，直接使用 rule-based verifier 而非 reward model。规则奖励公式如下：

$$R_{\text{rule}}(\hat{y},y) = \begin{cases} 1, & \mathrm{is\_equivalent}(\hat{y},y) \\ -1, & \text{otherwise} \end{cases}$$

其中，$y$ 为 ground-truth answer，$\hat{y}$ 为 predicted answer。

在 Overlong Reward Shaping 中，还会引入 $R_{\text{length}}(o_{i})$，故 response-level reward/return $R(q,a,o_{i}) = R_{\text{rule}}(a,o_{i}) + R_{\text{length}}(o_{i})$。优势计算如下：

$$\hat{A}_{i,t} = \hat{A}_{i} = \frac{R(q,a,o_{i}) - \mathrm{mean}(\{R(q,a,o_{j})\}_{j=1}^{G})}{\mathrm{std}(\{R(q,a,o_{j})\}_{j=1}^{G})}$$

Clip-Higher

Clip-Higher 针对熵坍缩问题，通过解耦 clip 上下界 $\epsilon_{\text{low}}$,$\epsilon_{\text{high}}$ 以鼓励模型探索。传统 PPO 对 policy ratio $r_{t}(\theta)$ 进行对称裁剪（e.g., $[1-\epsilon,1+\epsilon]$, $\epsilon=0.2$）可能限制低概率 exploration token 的增加，而 Clip-Higher 保持下界 $\epsilon_{\text{low}} = 0.2$ 不变，扩大上界 $\epsilon_{\text{high}} = 0.28$。

Dynamic Sampling

在 GRPO 中，当一个 question $q$ 生成的所有 $G$ 个 answer 全都正确（奖励均为 $+1$）或全都错误（奖励均为 $-1$）时，group 内奖励均值均为 $+1$ 或 $-1$，进而这 $G$ 个样本的优势均为 $0$。因此，这个 group 中所有样本无法产生有效梯度信号，对模型更新毫无贡献。

Dynamic Sampling 的核心思想是：只用能产生有效梯度的样本进行训练。DAPO 通过在目标函数中添加一个约束条件来实现：

$$\text{s.t.}\quad 0 < | \{ o_{i} \mid \mathrm{is\_equivalent}(a,o_{i}) \} | < G$$

这个约束的含义是，对于每个 question $q$，其生成的 $G$ 个 answer 中，必须既有正解，也有错解。当均为正解时，$| \{ o_{i} \mid \mathrm{is\_equivalent}(a,o_{i}) \} | = G$；当均为错解时，$\{ o_{i} \mid \mathrm{is\_equivalent}(a,o_{i}) \} | = 0$。

Token-Level Policy Gradient Loss

原始的 GRPO 算法采用 sample-level loss。它首先计算每个 response 内所有 token 损失均值，再计算 batch 内所有 response 损失均值。在这种权重下，每个样本，不论长短，对最终总损失的贡献是均等的。在 long-CoT 场景中，存在两个问题：

1. 长样本中每个 token 的权重被稀释了，使得模型难以从高质量的长推理过程中充分学习其内在模式。
2. 过长样本中常常包含无意义的重复与胡言乱语的 token。由于权重被稀释，sample-level loss 无法有效惩罚这些低质量模式，导致模型生成熵和响应长度不受控制地 " 野蛮生长 "

与 GRPO 先对 response 求均值，再对 batch 求均值不同，DAPO 将 batch 内所有 response 的所有 token loss 直接求均值。具体来说，将目标函数中的 $1/|o_{i}|$ 外置变成 $1/\sum_{i=1}^{G}|o_{i}|$。这样，损失的计算变成 token-level，每个 token 对最终梯度更新的贡献是平等的，无论 response 的长短。

Overlong Reward Shaping

在 RL-tuning 中，通常会设定一个最大生成长度，超出长度的 response 会被截断。然而，一个可能包含完全正确推理过程的 response，因为尚未出现正确答案（e.g., \boxed{}）而被截断，导致规则奖励为 $-1$，这会引入 reward noise，让模型误以为其正确的推理路径是错误的。

DAPO 探索了两种途径，一种是 Overlong Filtering，直接将被截断的样本的损失 mask 掉，使它们不参与梯度计算，已经能稳定训练并提升性能。另一种是 Soft Overlong Punishment，设计一个长度惩罚如下：

$$R_{\text{length}}(y) = \begin{cases} 0, & |y| \le L_{\text{max}} - L_{\text{cache}} & \text{Case 1: Safe Zone} \\ \frac{(L_{\text{max}} - L_{\text{cache}}) - |y|}{L_{\text{cache}}}, & L_{\text{max}} - L_{\text{cache}} < |y| \le L_{\text{max}} & \text{Case 2: Soft Punishment Buffer} \\ -1, & |y| > L_{\text{max}} & \text{Case 3: Hard Punishment Zone} \end{cases}$$

其中：

• $|y|$: 生成样本 $y$ 的实际长度
• $L_{\text{max}}$: 预设的最大长度上限。我们希望当模型超过该长度后，会渐进受到惩罚。
• $L_{\text{cache}}$: 缓冲区长度

注意，这里 $L_{\text{max}}$ 并非 rollout 阶段，传递给推理引擎的物理参数 max_tokens。实际上，该论文实验设定 $L_{\text{max}}=16,384$, $L_{\text{cache}}=4,096$。因此，最大生成 token 数应该为 $L_{\text{max}} + L_{\text{cache}} = 20,480$。

此时，我们来详细解读长度惩罚函数的三个阶段：

1. 第一阶段：安全区（$0 < |y| \le 12,288$）。此时，模型有充足的长度来进行必要的推理，不会受到任何惩罚
2. 第二阶段：软惩罚区（$12,288 < |y| \le 16,384$）。该长度惩罚是个线性函数，当长度刚进入此区间时，不会受到惩罚（$R_{\text{length}} = 0$）；当长度即将达到 $L_{\text{max}}$ 时，惩罚接近 $-1$。这个规则希望模型在保证正确性的前提下，尽量避免生成过长的回答，但又不像硬截断那样引入剧烈的噪声。
3. 第三阶段：硬惩罚区（$16,384 < |y| \le 20,480$）。任何超过 $L_{\text{max}}$ 长度的回复，长度惩罚均为 $-1$

该长度惩罚会直接添加到规则奖励中，最终的奖励函数为 $R(q,a,o_{i}) = R_{\text{rule}}(a,o_{i}) + R_{\text{length}}(o_{i})$。可以推测，当回复达到物理最大生成长度，即 $|y| >20,480$ 时，会被截断。此时，不仅要受到规则奖励 $-1$，还会受到长度惩罚 $-1$

CISPO: Clipped IS-weight Policy Optimization

MiniMax-M1 技术报告中提出了 CISPO 算法，该算法主要解决 PPO/GRPO 中存在的 token clipping 问题。具体来说，一些与反思行为有关的 token (e.g., “However”, “Recheck”, “Wait”, “Aha”) 会充当推理路径中的分叉，但它们的概率通常在 base model 中很稀有。而在策略更新时，这些 token 会表现出较高的 $r_{i,t}(\theta)$。因此，在第一次 on-policy 梯度更新后，这些 token 会被裁剪掉，阻止了后续的 off-policy 梯度更新。然而，这些低概率的 token 对于稳定策略熵很重要。

接下来，具体距离来分析这一问题。PPO/GRPO 目标函数中核心项如下：

$$\min\Big( r_{i,t}(\theta) \hat{A}_{i,t}, \mathrm{clip}\big(r_{i,t}(\theta),1-\epsilon,1+\epsilon\big)\hat{A}_{i,t} \Big)$$

第一次 on-policy 梯度更新时，由于 $\pi_{\theta}=\pi_{\theta_{old}}$，则 $r_{i,t}(\theta)=1$，故不会被裁剪。在此之后的第二次 off-policy 更新，假设 token 的 $r_{i,t}(\theta)=2$，而 $\epsilon=0.2$，则最终会走 $1+\epsilon=1.2$ 这个常数分支，$\mathrm{clip}$ 函数反向传播给 $r_{i,t}(\theta)$ 的梯度则为 $0$。因此，当一个 token 的更新因为 $r_{i,t}(\theta)$ 过大而被裁剪时，从该 token 流向 $\theta$ 的梯度则为 $0$。这也是为什么 DAPO 采取了 Clip-Higher 的操作。那么当 $r_{i,t}(\theta)$ 较小时，不妨设 $r_{i,t}(\theta)=0.5$。此时，并不会走到 $1-\epsilon=0.8$ 这个常数分支，反向传播给 $\theta$ 的梯度信号依然存在。这也是为什么 DAPO 并不调节 $\epsilon_{\text{low}}$，仅扩大上界 $\epsilon_{\text{high}}$。

为了解决这一问题，CISPO 不对 token 更新本身进行裁剪，而是直接裁剪 IS weight (a.k.a., policy ratio) $r_{i,t}(\theta)$，从而保证所有 token，无论其 $r_{i,t}(\theta)$ 多大，梯度信号都会存在，用于策略参数更新。首先，回顾 vanilla REINFORCE 的 offline 目标函数：

$$J(\theta) = \mathbb{E}_{(q,a) \sim p_{\mathcal{Q}},o \sim \pi_{\theta_{old}}(\cdot \mid q)}\Bigg[ \frac{1}{|o_{i}|}\sum_{t=1}^{|o_{i}|} \mathrm{sg}(r_{i,t}(\theta)) \hat{A}_{i,t} \log \pi_{\theta}(o_{i,t} \mid q,o_{i,<t}) \Bigg]$$

其中，$\mathrm{sg}(\cdot)$ 表示 stop-gradient。这是因为在标准策略梯度算法中，参与求导的只有 $\log \pi_{\theta}$，而 policy ratio 在当前步只是作为常量缩放因子，用于修正分布差异，其自身并不参与梯度计算。类似不参与梯度计算的还有优势 $\hat{A}_{i,t}$。此外，上式中的长度归一化项 $1/|o_{i}|$ 并不是标准的策略梯度算法，具体分析见 Dr. GRPO。

接下来，基于 GRPO，给出 CISPO 算法的目标函数：

$$J(\theta) = \mathbb{E}_{(q,a) \sim p_{\mathcal{Q}},\{o_{i}\}_{i=1}^{G} \sim \pi_{\theta_{old}}(\cdot \mid q)}\Bigg[ {\color{red}\frac{1}{\sum_{i=1}^{G}|o_{i}|}} \sum_{i=1}^{G} \sum_{t=1}^{|o_{i}|} \mathrm{sg}({\color{red}\hat{r}_{i,t}(\theta)}) \hat{A}_{i,t} \log \pi_{\theta}(o_{i,t} \mid q,o_{i,<t}) \Bigg]$$

其中，优势近似 $\hat{A}_{i,t}$ 与 GRPO 保持一致，$\hat{r}_{i,t}(\theta)$ 是 clipped IS weight:

$$\hat{r}_{i,t}(\theta) = \mathrm{clip}(r_{i,t}(\theta),1-\epsilon_{\text{low}}^{\text{IS}},1-\epsilon_{\text{high}}^{\text{IS}})$$

在实验中，不设置 IS weight 的下限，即将 $\epsilon_{\text{low}}^{\text{IS}}$ 设置较大值，主要调节 $\epsilon_{\text{high}}^{\text{IS}}$。

此外，CISPO 也利用了 DAPO 的 dynamic sampling 与 length penalty 技术，同时移除了 KL 惩罚。

最后，通过在目标函数中引入一个 token-wise mask $M_{i,t}$ 来统一 CISPO/PPO/GRPO:

$$J(\theta) = \mathbb{E}_{(q,a) \sim p_{\mathcal{Q}},\{o_{i}\}_{i=1}^{G} \sim \pi_{\theta_{old}}(\cdot \mid q)}\Bigg[ \frac{1}{\sum_{i=1}^{G}|o_{i}|} \sum_{i=1}^{G} \sum_{t=1}^{|o_{i}|} \mathrm{sg}(\hat{r}_{i,t}(\theta)) \hat{A}_{i,t} \log \pi_{\theta}(o_{i,t} \mid q,o_{i,<t}) {\color{red}M_{i,t}} \Bigg]$$

其中，mask $M_{i,t}$ 相当于 PPO 的 trust region，定义如下：

$$M_{i,t} = \begin{cases} 0, & \hat{A}_{i,t} > 0 \text{ and } r_{i,t}(\theta) > 1 + \epsilon_{\text{high}} \\ 0, & \hat{A}_{i,t} < 0 \text{ and } r_{i,t}(\theta) < 1 + \epsilon_{\text{low}} \\ 1, & \text{otherwise} \end{cases}$$

观察上式可知，$M_{i,t} = 0$ 的两组条件，恰好对应了 PPO/GRPO 中的核心项：

$$\min\Big( r_{i,t}(\theta) \hat{A}_{i,t}, \mathrm{clip}\big(r_{i,t}(\theta),1-\epsilon,1+\epsilon\big)\hat{A}_{i,t} \Big)$$

而当 $M_{i,t} = 1$ 时，恰好是 CISPO 的标准形式。

总结 PPO/GRPO 与 CISPO token-level 梯度信号控制的思路对比：前者可以概括为，当某个 token $r_{i,t}(\theta)$ 过大时，直接进行硬截断，不会对策略梯度有贡献；而后者通过裁剪 $r_{i,t}(\theta)$ 到一个预设的范围，所有 token 都会对策略梯度有贡献。

Reference

对于本文的符号使用，主要参考 Dr. GRPO 的论文，后面会列出。

对于 RL4LLM 进展梳理的文章已经有很多，笔者写作时都有参考：

• Policy Gradient Algorithms | RLHF Book by Nathan Lambert
• 万字长文梳理RL最新进展：从policy gradient到GRPO, REINFORCE++, StableReinforce - 知乎
• 一文对比4种 RLHF 算法：PPO, GRPO, RLOO, REINFORCE++ - 知乎
• RLHF 及其变体 Iterative DPO/RLOO/GRPO/REINFORCE 算法和工程分析 - 知乎
• 【AI Infra】【RLHF框架】四、VeRL中PPO、GRPO、REINFORCE++、RLOO实现源码解析 - 知乎

对于各个算法的论文原文及论文解读，列举如下：

• PPO
  • 传统 RL 中的 PPO: [1707.06347] Proximal Policy Optimization Algorithms
  • OpenAI 将 PPO 引入 RLHF: [2009.01325] Learning to summarize from human feedback
• RLOO
  • 将 RLOO 引入 RLHF: [2402.14740] Back to Basics: Revisiting REINFORCE Style Optimization for Learning from Human Feedback in LLMs
  • HuggingFace Blog：Putting RL back in RLHF 中文版：将强化学习重新引入 RLHF - 知乎
  • 结合代码解读：RLOO论文笔记 & TRL rloo_trainer源码简析 - 知乎
• ReMax
  • 论文原文：[2310.10505] ReMax: A Simple, Effective, and Efficient Reinforcement Learning Method for Aligning Large Language Models
  • 作者自己的博文: ReMax: 一种高效，可替代PPO的RLHF算法 (ICML2024) - 知乎
• GRPO
  • 论文原文：[2402.03300] DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models
  • 从零实现 DeepSeek Aha Moment: nanoAhaMoment: RL for LLM from Scratch with 1 GPU - Part 1 - YouTube
• Dr. GRPO
  • 论文原文：[2503.20783] Understanding R1-Zero-Like Training: A Critical Perspective
  • 与 DAPO 对比解读：异曲同工之妙的DrGRPO——DAPO几乎同时出现的又一GRPO优化！ - 知乎
• REINFORCE++
  • 论文原文：[2501.03262] REINFORCE++: An Efficient RLHF Algorithm with Robustness to Both Prompt and Reward Models
  • 作者自己的博文：RLHF 对齐之 REINFORCE++ 算法 - 比 GRPO 稳定比PPO快 - 知乎 英文版 REINFORCE++: A Simple and Efficient Approach for Aligning Large Language Models
• DAPO
  • 论文原文：[2503.14476] DAPO: An Open-Source LLM Reinforcement Learning System at Scale
  • 论文解读：DAPO：为GRPO的锦上加四点花 - 知乎
• CISPO
  • MiniMax-M1 技术报告中首次提出 CISPO: [2506.13585] MiniMax-M1: Scaling Test-Time Compute Efficiently with Lightning Attention
  • 深入熵角度进行解读：GRPO优化在继续——CISPO和熵 - 知乎