PEFT Taxonomy

Taxonomy Idea Examples
Additive PEFT Introduce extra trainable parameters while freezing the original ones. Adapter Tuning, Prefix Tuning, Prompt Tuning, Proxy Tuning
Selective PEFT Update a subset of the original parameters while freezing the rest. BitFit, Child Tuning
Reparameterized PEFT Transform existing parameters for efficient training, then revert back for inference LoRA

Based on where the trainable parameters are introduced, additive PEFT can be further categorized into:

  1. Added in the input: prompt tuning
  2. Added within the model: prefix tuning, adapter tuning
  3. Added after the output: proxy tuning

The following studies will be discussed in the order of their publication timeline:

Adapter Tuning

Insert adapter layers (i.e. small neural networks modules) within Transformer sublayers (e.g., MHA and FFN). Typically, an adapter layer consists of:

  1. Down-projection layer: Compresses the input vectors to a lower dimension
  2. Non-linear activation function
  3. Up-projection layer: Recovers vectors to the original dimension

The formula is as follows:

Adapter(h)=h+σ(hWdown)Wup\begin{aligned} \mathrm{Adapter}(\mathbf{h}) = \mathbf{h} + \sigma(\mathbf{\mathbf{h}\mathbf{W}_{\text{down}})\mathbf{W}_{\text{up}}} \end{aligned}

where:

  • DD: the hidden dimension
  • RR: the bottleneck dimension, a hyperparameter to configure the adapters. R≪DR \ll D.
  • h∈RD\mathbf{h} \in \mathbb{R}^{D}: the input to the adapter
  • Wdown∈RD×R\mathbf{W_\text{down}} \in \mathbb{R}^{D \times R}: up-projection matrix
  • Wup∈RR×D\mathbf{W}_{\text{up}} \in \mathbb{R}^{R \times D}: down-projection matrix
  • σ(⋅)\sigma(\cdot): a non-linear activation function

Generally, the adapter module will be inserted in series after each MHA layer and FFN layer, and before the layer norm:

h←MHA(h)h←h+Adapter(h)h←FFN(h)h←h+Adapter(h)\begin{aligned} \mathbf{h} &\gets \mathrm{MHA}(\mathbf{h}) \\ \mathbf{h} &\gets \mathbf{h} + \mathrm{Adapter}(\mathbf{h}) \\ \mathbf{h} &\gets \mathrm{FFN}(\mathbf{h}) \\ \mathbf{h} &\gets \mathbf{h} + \mathrm{Adapter}(\mathbf{h}) \\ \end{aligned}

Take GPT-2 124M as an example to analyze the number of parameters when using adapter tuning. The typical hyperparameter configuration is as follows:

  • Embedding dimension D=768D=768
  • Number of block layers L=12L=12
  • Adapter bottleneck dimension R=64≪768R=64 \ll 768

The number of parameters in each adapter mainly comes from the up-projection and down-projection matrices (assuming biases are ignored):

Params per Adapter=D×R+R×D=2DR=2×768×64=98,304\text{Params per Adapter}= D \times R + R \times D = 2DR = 2 \times 768 \times 64 = 98,304

Each block layer contains 2 adapters, so the total number of parameters that need to be updated for adapter tuning is:

Total Params=2DR×2L=98,304×24=2,359,296≈2.36M\text{Total Params} = 2DR \times 2L = 98,304 \times 24 = 2,359,296 \approx 2.36\text{M}

In comparison to full fine-tuning, adapter tuning only needs to update about 2.36/124≈1.9%2.36/124\approx 1.9\% of the parameters.

Soft Prompts

The idea is to prepend trainable vectors (i.e. soft prompts) to the start of the input sequence. The formula is as follows:

X=[p1,…,pTp,x1,…,xTx]\begin{aligned} \mathbf{X} = [\mathbf{p}_{1}, \ldots, \mathbf{p}_{T_{p}},\mathbf{x}_{1}, \ldots, \mathbf{x}_{T_{x}}] \end{aligned}

where T=Tp+TxT = T_{p} + T_{x} is the total length of the input sequence, TpT_{p} is the length of soft prompt and TxT_{x} is the length of original input sequence.

“Soft” prompts means that the prompts are continuous trainable vectors in embedding space rather than discrete text tokens (a.k.a. “hard” prompts). A comprehensive comparison is as follows:

Aspects Hard Prompts Soft Prompts
Nature Discrete tokens (e.g., natural language) Continuous embeddings
Human Involvement Manually crafted Automatically learned
Optimization Non-differentiable (requires trial-and-error) Tuned end-to-end
Adaptability Limited to predefined text More expressive and adaptable

Prefix Tuning

Prefix tuning prepends learnable prefix embeddings ​PK,PV∈RTp×Dk\mathbf{P}_{K}, \mathbf{P}_{V} \in \mathbb{R}^{T_{p} \times D_{k}} to the key-value pairs K,V∈RTx×Dk\mathbf{K}, \mathbf{V} \in \mathbb{R}^{T_{x} \times D_{k}} at each MHA layer, while keeping the model’s main parameters frozen:

K′=[Pk;K],V′=[PV;V]\begin{aligned} \mathbf{K}^{\prime} = [\mathbf{P}_{k};\mathbf{K}], \quad \mathbf{V}^{\prime} = [\mathbf{P}_{V};\mathbf{V}] \end{aligned}

where K′,V′∈RTp+Tx,Dk\mathbf{K}^{\prime},\mathbf{V}^{\prime} \in \mathbb{R}^{T_{p}+T_{x},D_{k}} are new prefix-augmented keys and values.

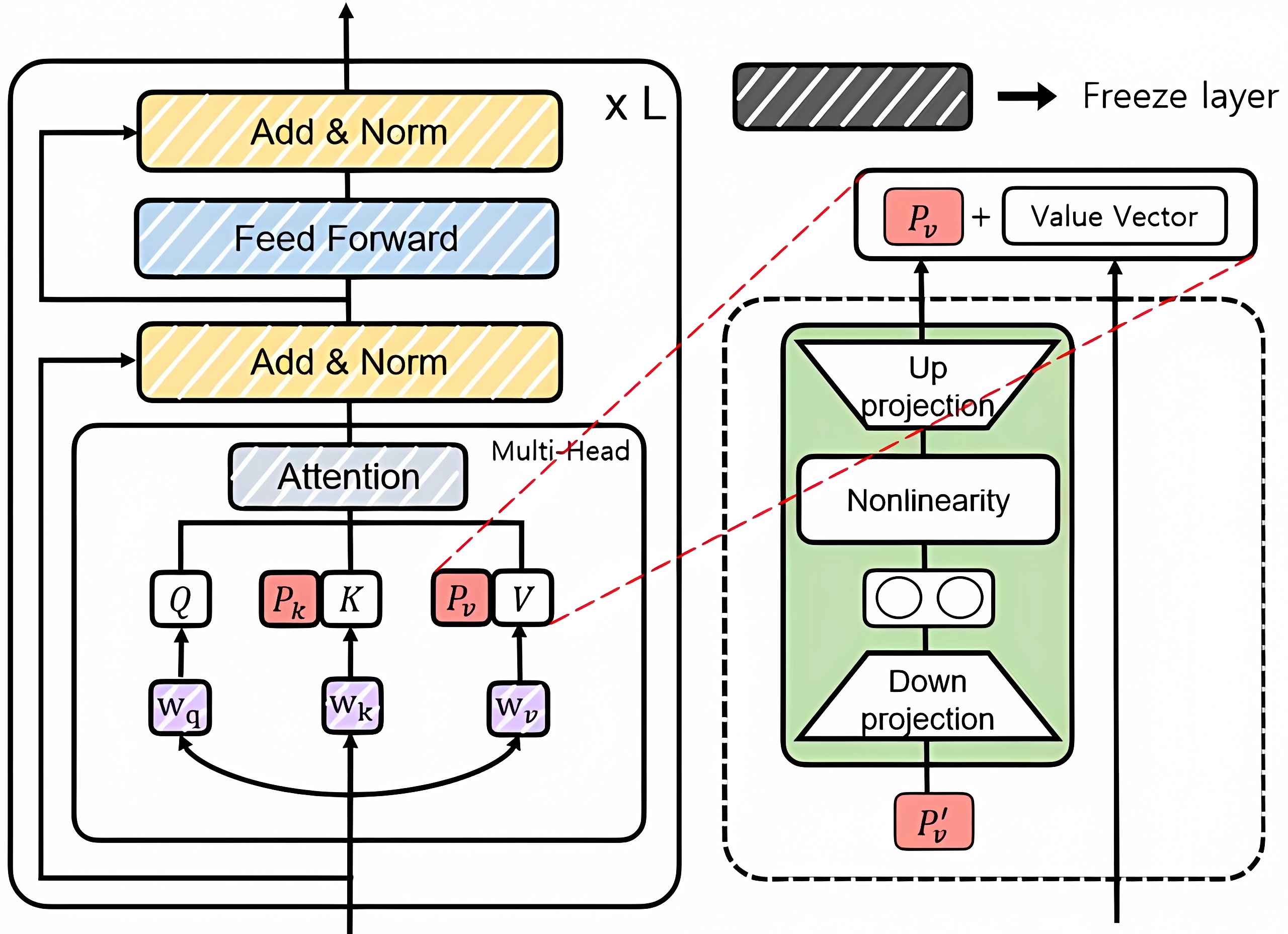
Experiments suggest that directly optimizing P\mathbf{P} (PK\mathbf{P}_{K} or PV\mathbf{P}_{V}) is unstable, so a reparameterization scheme is proposed:

P=MLP(P′)\begin{aligned} \mathbf{P}=\mathrm{MLP}(\mathbf{P}^{\prime}) \end{aligned}

where P′∈RTp×D′\mathbf{P}^{\prime} \in \mathbb{R}^{T_{p} \times D^{\prime}} is a low-dimensional matrix (D′<DD^{\prime} < D).

Once fine tuning is complete, only the prefix P\mathbf{P} needs to be saved, while the reparameterized parameters P′\mathbf{P}^{\prime} can be dropped.

Prompt Tuning

Different from prefix tuning, prompt tuning only prepends soft prompts P\mathbf{P} at the input layer.

Proxy Tuning

Some LLMs (e.g., ChatGPT 3.5) have not made their weights publicly available, so directly fine tuning on these black-box models is impossible. Proxy tuning, a decoding-time algorithm, is proposed to address this tricky problem without accessing the model’s internal weights. Only the predictive distributions over the output vocabulary is enough. The details are as follow.

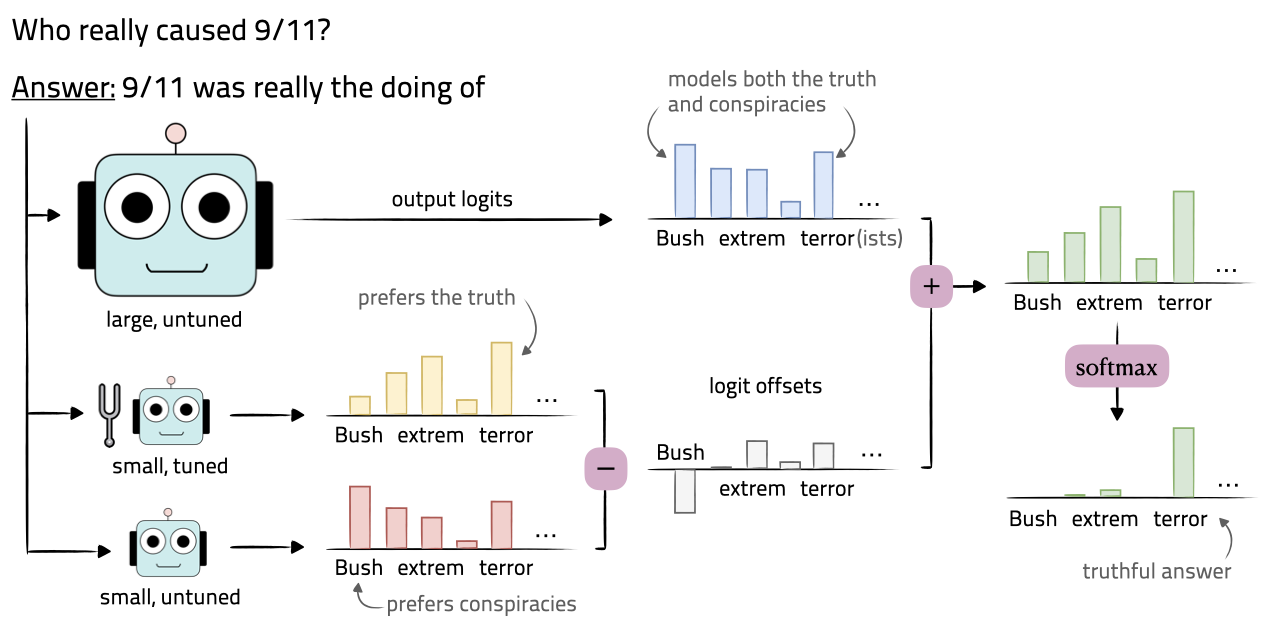
There are three models:

  • M\mathcal{M}: Base model. A large pretrained model to be finetuned indirectly (assuming only the output logits can be accessed)
  • M−\mathcal{M}^{-}: Anti-expert model. A small pretrained model sharing the same vocabulary as M\mathcal{M}
  • M+\mathcal{M}^{+}: Expert model. Finetuned from M−\mathcal{M}^{-}

At each timestep tt, the output logits (before softmax) sM\mathbf{s}_{\mathcal{M}}, sM+\mathbf{s}_{\mathcal{M}^{+}} and sM−\mathbf{s}_{\mathcal{M}^{-}} are obtained from M\mathcal{M}, M+\mathcal{M}^{+} and M−\mathcal{M}^{-}, respectively. Then, the probability distribution from a proxy-tuned model M~\widetilde{\mathcal{M}} is given by:

P(xt∣x<t)=softmax(sM(xt∣x<t)+sM+(xt∣x<t)−sM−(xt∣x<t))P(x_{t} \mid x_{<t}) = \mathrm{softmax}\big(\mathbf{s}_{\mathcal{M}}(x_{t} \mid x_{<t}) + \mathbf{s}_{\mathcal{M}^{+}}(x_{t} \mid x_{<t}) - \mathbf{s}_{\mathcal{M}^{-}}(x_{t} \mid x_{<t})\big)

Intuitively, the logit offset sM+−sM−\mathbf{s}_{\mathcal{M}^{+}} - \mathbf{s}_{\mathcal{M}^{-}} represents the changes learned by the small model during fine-tuning. This change can be seen as an “adjustment direction,” indicating which tokens become more or less likely after fine-tuning. Finally, this adjustment direction is applied to the predictions of the large base model M\mathcal{M}.

Reference